导数的基本公式 常见函数的导数有哪些公式

导数的基本公式有哪些

导数在数学特别是微积分里可是超级重要的工具，说到导数公式，咱们得先掌握几个“杀手锏”，这样以后遇到各种问题才能轻松应对。这里整理了14个基本公式，快来看看吧：

1. y=c，导数是0（因为常数函数的斜率永远是零嘛）。
2. y=x^μ，导数就是μx^(μ－1)，这里的μ是常数且不等于0。
3. 指数函数：y=a^x的导数是a^x乘以ln(a)，特别地，y=e^x的导数就是它本身，超级酷对吧！
4. 对数函数里，y=log_a x的导数是1除以x再乘以ln(a)的倒数；特别是自然对数lnx，导数就是1/x。
5. 三角函数超经典：y=sinx的导数是cosx；y=cosx的导数是负sinx。
6. 还有y=tanx的导数是( sec x ) 的平方，至于余切cotx，导数是负的(csc x)平方。
7. 其他导数如secx的导数是secx乘以tanx，cscx的导数是负cscx乘以cotx。

这14个公式就像是你的“万能钥匙”，找到它们，很多问题都能迎刃而解！

常见函数的导数公式怎么整理

说完了基本的导数，你知道常见函数的导数公式是咋整的吗？其实挺规律的，我帮你按编号捋出来，让人一看就明白：

1. 三角函数：
   - （sinx）' = cosx，也就是正弦的导数是余弦；
   - （cosx）' = -sinx，余弦的导数是正弦的相反数；
   - （tanx）' = (secx)^2，正切的导数是正割平方；
   - （cotx）' = -(cscx)^2，余切的导数是余割平方的相反数；
   - （secx）' = secx·tanx，正割曲线的导数；
   - （cscx）' = -cscx·cotx，余割的导数。

2. 指数与对数函数：
   - y=a^x，导数是a^x乘以ln(a)；
   - y=e^x，导数还是它自己，没错，多好记；
   - y=log_a x的导数是1/(x ln a)；
   - y=ln x的导数就是1/x。

3. 幂函数和常数函数：
   - 常数函数y=c，导数必为0；
   - 幂函数y=x^n，导数是nx^(n-1)。

4. 复合与分式求导技巧：
   - 复合函数y=f[g(x)]的导数等于f'在g(x)处乘以g'(x)，这里对g(x)当作整体变量别搞混；
   - 分式函数y=u/v的求导是(u'v - uv') / v^2。

是不是感觉这些知识点就像搭积木，一块接着一块变得越来越牢固？其实，掌握了这些公式，你就能在数学海洋中畅游无阻啦！

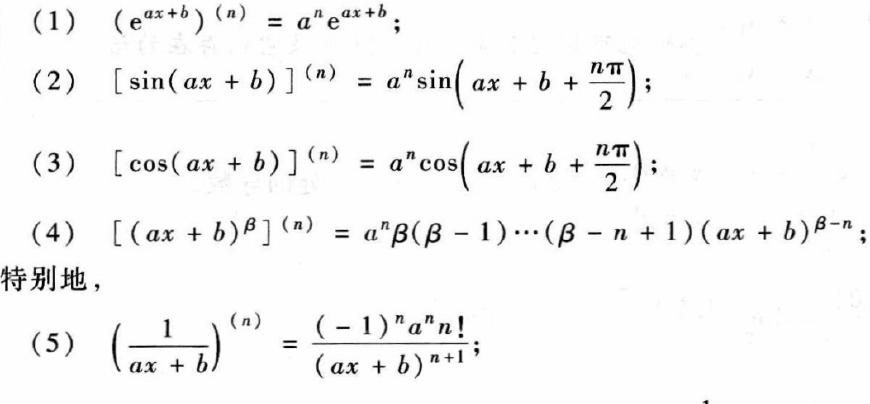
相关问题解答

1. 导数公式有哪些是最基础且必须记住的？
   哎呀，这个问题问得好！其实，最基础的有：常数函数导数是0，幂函数的求导（nx^(n-1)那条），指数函数尤其是e^x的导数，还有三角函数sinx和cosx的导数。这几个就像数学里的“常青树”，学会了之后再熟悉其他公式时会轻松许多！记住它们，后面遇到复杂问题也能有底气冲刺！

2. 三角函数的导数为什么这么重要？
   说真的，三角函数在物理和工程里用得特别多！比如波动、振动啥的，sin和cos就必不可少。掌握它们的导数，你不仅能搞定考试，还能理解现实中很多现象。所以，别小看sin和cos的导数，学好了以后你会感谢自己的！

3. 复合函数的链式法则怎么用才顺手？
   哈哈，链式法则其实就是拆包裹的感觉。先看外层函数的导数，再乘以内层函数的导数。比如你看到一个y=f(g(x))，先把g(x)当成新变量求f'，然后别忘了乘以g'(x)，两步走。多做练习，慢慢你会觉得这招超简单，眼一闭都能做出来呢！

4. 对数函数导数的数学意义是什么呢？
   这个嘛，导数1/x意味着当x越大，y=ln x的变化率会逐渐变小。生活中也有类似情况，比如花费和效益的比例关系。理解它能帮助你深刻体会变量间变化快慢。简单说，ln x的导数告诉你这个函数长得多“缓”，非常实用哦！