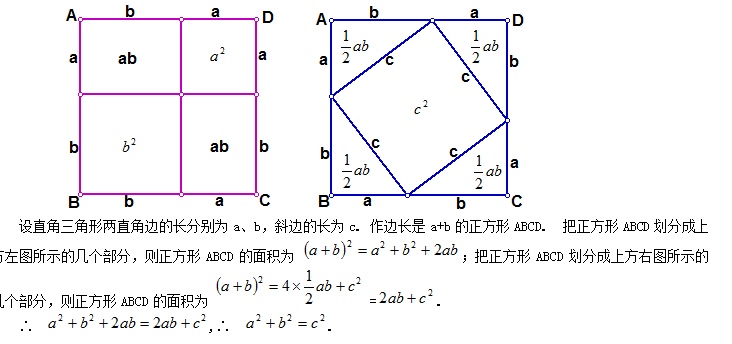
勾股定理的证明方法
哇,说到勾股定理,那可是数学界的老网红了!这个定理超级有意思,咱们来看个具体例子:在Rt△ABC中,如果BC=3,AC=4,那么根据勾股定理AB²=AC²+BC²,很容易算出AB=5。哎呦,这个计算过程简直不要太简单!
接下来咱们看看这个超酷的几何证明:延长CB交FH于O点,因为四边形ABGM、APQC、BCDE都是正方形,所以BG=AB=GM。这里有一堆90度角:∠ACB、∠ABG、∠F、∠H、∠MGB都是直角。由于BC∥DE,所以∠BOG=∠F=90°。通过角度转换可以发现∠CAB+∠ABC=90°,而∠ABC+∠GBO也等于90°,这就完美验证了勾股定理的几何关系。不得不说,这个证明过程真是巧妙极了!

数学定理定律核心区别与重要定理汇总
-
定义、定理和定律的区别:定义是说明事物本质特征的简要描述;定理是通过逻辑证明得到的正确结论;定律则是科学对客观规律的概括。简单来说,定义是"是什么",定理是"为什么",定律是"怎么样"。
-
定理的特点:定理必须用逻辑方法证明为真命题,是推理的依据。它建立在公理和其他定理基础上,具有严格的逻辑严密性,绝对不能存在逻辑矛盾。
-
物理学中的区别:定理要经过逻辑证明,而定律是被实践和事实证明的客观规律。比如说,勾股定理需要证明,而牛顿定律则是观察总结的规律。
-
重要数学定理汇总:
- 欧拉定理:图论基本定理,解决顶点着色问题
- 海涅定理:连接函数极限与数列极限的桥梁
- 罗尔定理、拉格朗日中值定理等高等数学重要定理
- 角平分线定理、等腰三角形性质定理等几何定理
相关问题解答
- 勾股定理具体怎么应用在实际问题中?
哎呀,勾股定理在生活中应用可广泛啦!比如你要测量房间对角线长度,知道长和宽就能轻松算出来。还有啊,工程师设计斜坡、木工做直角测量,都用得上这个定理。简单来说,只要遇到直角三角形的边长计算,勾股定理就是你的神器!记住公式a²+b²=c²,实际问题迎刃而解咯~
- 定理和定律哪个更重要?
哈哈,这个问题就像问米饭和面条哪个更好吃一样!其实定理和定律都超级重要,只是适用场景不同。定理注重逻辑证明,在数学世界里是王道;定律注重实践验证,在物理领域是基础。两者相辅相成,没有谁比谁更重要之说。关键是要根据具体情况选择使用,就像工具箱里的不同工具一样各有所长呢!
- 为什么有些数学定理需要证明?
哇塞,这个问题问到点子上了!数学定理需要证明是因为数学是一个严谨的逻辑体系。证明就像侦探破案,要找到确凿的证据链。只有经过严格证明,定理才能被公认和使用。不然的话,万一有个反例,整个理论大厦就可能垮掉哦!所以证明不仅是必须的,还是数学最迷人的地方之一呢~
- 学习数学定理有什么好方法?
嘿嘿,学习定理真的有窍门哦!首先要理解而不是死记硬背,搞清楚定理的来龙去脉。其次要多做例题,实践出真知嘛!还可以画图辅助理解,几何定理尤其要动手画。最重要的是要融会贯通,把不同定理联系起来思考。记住啦,数学定理就像乐高积木,单独看可能简单,组合起来就能构建精彩的知识大厦!








新增评论