三角函数的基本值是怎么定的
说到三角函数的值,咱们得先搞清楚这些值是咋来的。三角函数主要有三大类:正弦(sin)、余弦(cos)和正切(tan),它们的值都是由角度决定的。比如说,0°、30°、45°、60°、90°等这些特殊角度,它们的三角函数值非常经典,大家平时学数学时最常碰到。
举个例子:
- 0°时,sin0°=0,cos0°=1,tan0°=0;
- 90°时,sin90°=1,cos90°=0,tan90°是没定义的,没错,就是“无穷大”的意思哈,因为你不能把一个数除以0嘛。
这些函数值不仅是靠数学公式算出来,还和单位圆紧密相关呢。简单来说,三角函数其实就是单位圆上的点坐标组合。尤其在工程测绘、航海和物理里面,这些函数值常常派上大用场。

哪些角度的三角函数值最常见且该如何记忆
好了,说完了基本原理,咱们来一个重磅干货大集合!这里给你整理了几个超常用的角度以及它们的sin、cos、tan值,让你一看就懂,轻松记住!
-
15°(π/12):
- sin15° = (√6 - √2)/4 ≈ 0.259
- cos15° = (√6 + √2)/4 ≈ 0.966
- tan15° = 2 - √3 ≈ 0.267 -
30°(π/6):
- sin30° = 1/2 = 0.5
- cos30° = √3/2 ≈ 0.866
- tan30° = √3/3 ≈ 0.577 -
45°(π/4):
- sin45° = √2/2 ≈ 0.707
- cos45° = √2/2 ≈ 0.707
- tan45° = 1 -
60°(π/3):
- sin60° = √3/2 ≈ 0.866
- cos60° = 1/2 = 0.5
- tan60° = √3 ≈ 1.732 -
75°(5π/12):
- sin75° = (√6 + √2)/4 ≈ 0.966
- cos75° = (√6 - √2)/4 ≈ 0.259
- tan75° = 2 + √3 ≈ 3.732 -
90°(π/2):
- sin90° = 1
- cos90° = 0
- tan90° 未定义
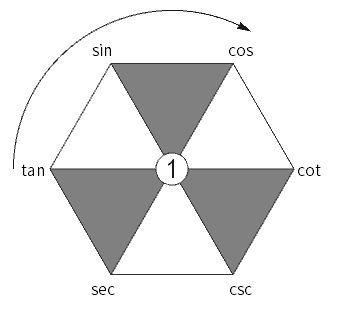
这些数值你要是背熟了,无论是解三角形还是验证公式,效率都会蹭蹭蹭往上涨呐!此外,还有一些冷门的结构函数,比如正割(sec)、余割(csc),它们是cos和sin的倒数。举个栗子,secθ=1/cosθ,cscθ=1/sinθ,能帮你快速变换公式,真心实用!
相关问题解答
-
三角函数为什么90度时正切函数没有定义呢?
哎呀,这个问题超级好玩!其实因为tanθ=sinθ/cosθ,当你角度是90度时,cos90°=0哎,分母为零啊,这可就尴尬了,对吧?数学里是叫“没定义”,咱们理解为“无穷大”啦,意味着值太大大到没法说清楚,你想象下数字炸裂的画面就行了,太震撼! -
有没有啥小妙招能帮我快速记住这些三角函数值?
嗯,给你支个招!想象单位圆上的点,顺时针转就是角度变化。还有“30、45、60度”的三角值有固定的漂亮平方根表达式,反复默写,结合图形记忆,超有效!再不行,就用一些口诀,比如“0,半,根二分之二,根三分之二,全”,反正多复习多用,肯定能记牢~ -
三角函数的正割和余割有什么用?
嘿,这哥俩其实就是余弦和正弦的“倒数兄弟”,用secθ=1/cosθ、cscθ=1/sinθ来表达。它们经常在高等数学和工程里亮相,特别方便用来简化复杂公式,绕开除零的尴尬。如果你想有更灵活的公式操作,这两兄弟绝对不可少啦! -
在学习三角函数时常见的坑有哪些?
哈哈,这个好多同学都会踩!比如把角度和弧度搞混,导致计算错乱;忘了tan90°无定义,硬要算结果;还有就是没搞清楚sin、cos哪个是哪个,计算题一不小心就翻车。建议老铁们多用图形辅助理解,多做练习题,一步步来,别急功近利,慢慢你会发现三角函数其实超有趣呢!

发表评论