欧拉函数是积性函数 欧拉函数怎样算

欧拉函数是什么积性函数是怎样证明的

欧拉函数，通常记作φ(n)，是指小于等于n且与n互质的正整数的个数。它拥有一个超级重要的性质——积性。你可能会问，什么是积性函数？简单来说，如果两个数m和n的最大公因数是1（也就是它们互质），那么欧拉函数满足φ(mn) = φ(m) × φ(n)，嘿，这可不是随便说说，而是有理有据的！

那么，咱们来聊聊为啥欧拉函数是积性函数吧。证明的关键就在于这：先定义f为一个函数，如果当m和n互质时满足f(mn) = f(m)f(n)，那么f就是积性的。欧拉函数φ(n)正是这样的函数。换句话说，利用数论里的互质性质和函数定义，我们能一步步证明φ(mn) = φ(m) × φ(n)，绝对没错！

这背后的思想挺妙的，它借助了“互质性”这个小秘密，让复杂的计算变得条理清晰，更重要的是这个性质帮助我们分解大问题为小问题，一步步来，简直太方便啦！

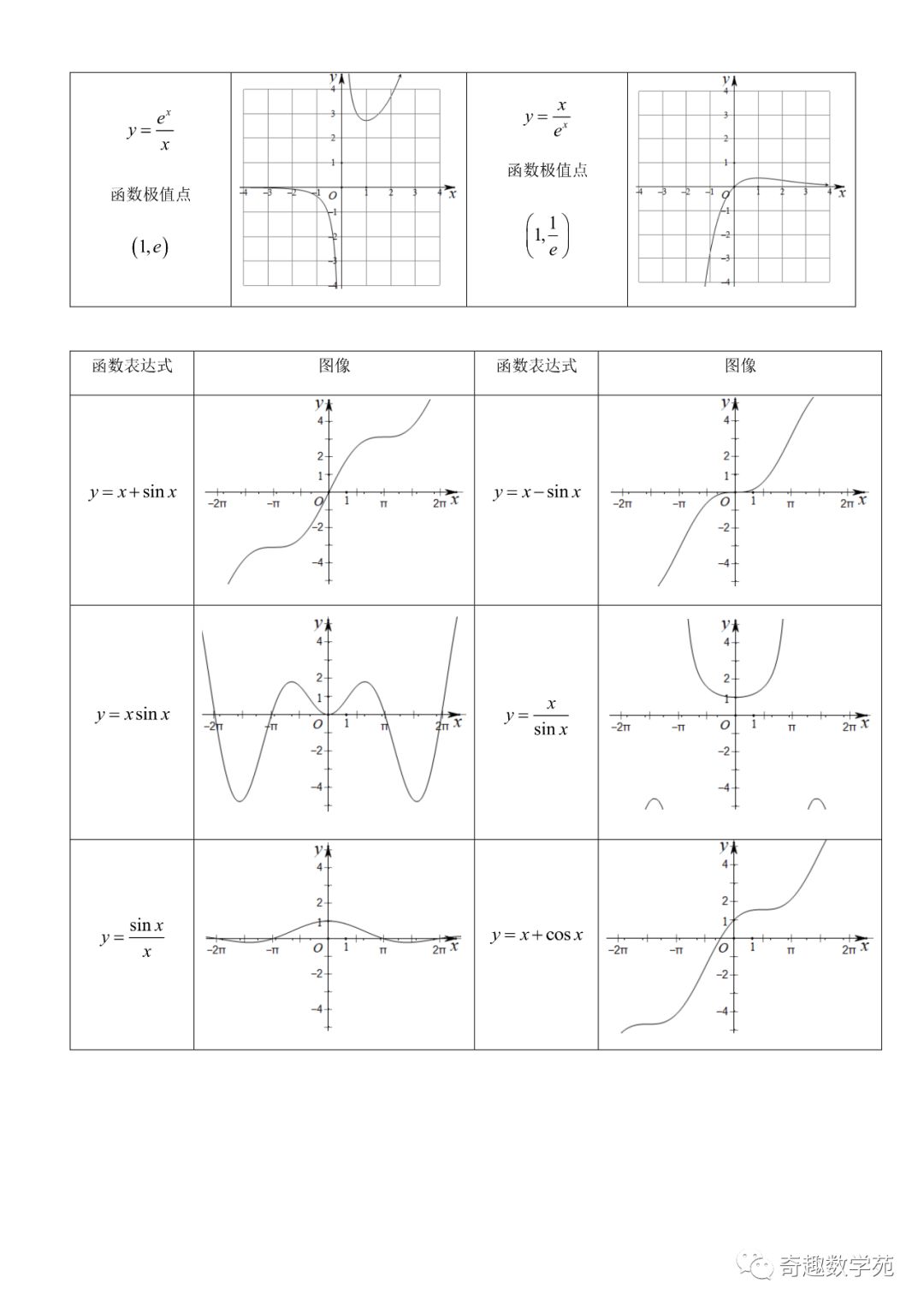
欧拉函数该怎么计算 计算方法和步骤全解析

说到欧拉函数的计算，你可得听我絮叨下，因为这里面可是有不少小窍门。

1. 质数幂的计算：假设有个数形如p^a，其中p是质数，a是正整数，那么φ(p^a) = p^a - p^(a-1)。为何这么算？其实就是说，从p的a次方到p的(a-1)次方之间的数不互质，而剩下的数字都是互质的，直接用这个公式非常方便。

2. 乘积分解计算：记住，任何正整数n都能分解成不同质数的乘积，比如说n = p1^a1 × p2^a2 × ... × pk^ak。欧拉函数的妙处就在于它能通过质数因子的分解，计算出φ(n) = n × Π(1 - 1/p)，这个采石场式的公式听着复杂，实际很牛掰！举个栗子，如果n=30，因子是2、3、5，那么φ(30) = 30 × (1-1/2) × (1-1/3) × (1-1/5) = 8。

3. 积性公式应用：利用刚才说的积性，你可以先计算φ(质数幂)，然后相乘，就能快速算出任何大数的欧拉函数，这不就是省时省力的神器吗？

4. 极限与数学分析的联系：顺带一提，欧拉函数随着n越来越大，φ(n)的值也会涨得很猛，这和数学分析里谈的无穷大、无穷小概念息息相关，数学家们可用这些关系深入研究数字的分布。

总之，算欧拉函数嘛，就是先找质因数，拿公式咔咔算，再用积性乘起来，so easy！

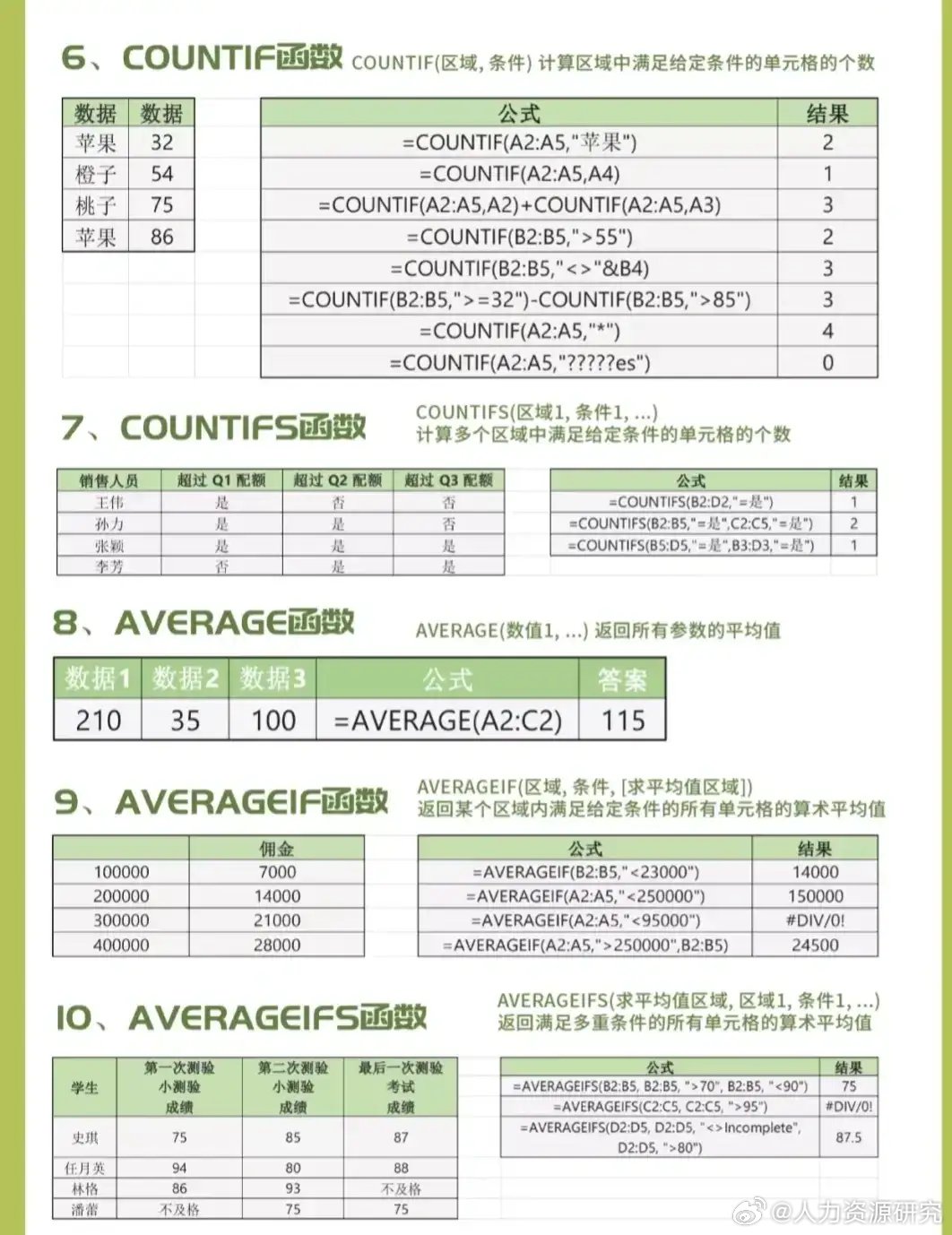
相关问题解答

1. 欧拉函数为什么是积性函数呢？
   哎呀，这个问题问得好！其实欧拉函数的积性本质上来自于互质的特性，换句话说，当两个数m和n没有共同因子时，它们的欧拉函数可以直接相乘，这就避免了重复计算重合部分。你可以想象成“互不干扰”，大家各自算，最后合起来。这背后的数学证明呢，就是通过定义和集合之间的映射关系一环扣一环，完美诠释什么才叫做“积性函数”，是不是瞬间感觉棒极啦！

2. 欧拉函数的计算公式怎么用才最简单？
   嘿，说到简单嘛，先把数字分解质因数，这可是必杀技！然后套用φ(n) = n × Π(1 - 1/p)的公式，大伙儿只要会分解质数，后面的乘法啥的简直小菜一碟。有些同学怕麻烦，建议记两个关键点：质数幂的公式和积性规律。这样，你只要动动手指，把数字拆开算，结果就能蹦出来，真是省时又省力。

3. 欧拉函数的极限值和数学分析有什么联系吗？
   太有趣了，这个问题！其实欧拉函数随着n变大，一直增长，这和数学里“无穷大”的概念有点儿像。更神奇的是，欧拉函数的增长速度和n本身的大小关系密切，通过极限分析，可以揭示数字的奥秘，比如分布密度这些东西，数学家超喜欢拿它来做深入研究。说白了，就是欧拉函数链接了整片数论和分析学的桥梁，酷炫吧！

4. 有没有简单的方法理解欧拉函数的定义？
   绝对有啦！换个通俗的方式想，欧拉函数就是数一下小于等于n且“和n没有关系”的数字有多少，嘿，怎么说“没有关系”呢？就是互质，没共享一个共同因子。你可以把它想成一次“筛选游戏”，从1到n，把所有和n有“牵手”关系的数字剔除，剩下的那部分就是φ(n)的值。简单又好记，是不是瞬间觉得数学没那么枯燥了！