指数函数怎么求导 指数函数的基本求导步骤是什么
指数函数的求导,我们先得明确一个基本的求导公式:如果函数是 ( y = a^x )(其中 ( a > 0 ) 且 ( a \neq 1 )),那么它的导数就是:
[
y' = ( \ln a ) \cdot a^x
]
这是数学中一个超重要的公式,记住它简直事半功倍!特别地,指数基础是自然对数的底数 ( e \approx 2.71828 ) 时,导数超级简单,就是函数本身:
[
\frac{d}{dx} e^x = e^x
]
就是说,咱们算导数的时候,( e^x )的变化率跟它值的大小完全一样。你看,简洁到飞起!
记得指数函数的定义有个小要求哦:指数位置的必须是自变量x,且前面系数只能是1,不能有别的复杂表达式,否则就不是纯指数函数啦。

指数函数和幂函数的求导操作步骤是什么 指数函数导数怎么具体计算
咱们来说说具体怎么求导吧,步骤其实不复杂,但得注意几个小细节:
-
变形为指数式:平时遇到像 ( z = x^y ) 这种函数,求对 ( y ) 的偏导数呢,一般会先利用公式 ( a^b = e^{b \ln a} ) 把原函数改写成指数幂的形式,这样方便求导。
-
对数两边取对数:然后对两边同时取自然对数,得到类似 ( \ln z = y \ln x ) 的表达式。
-
对变量求导:对改写后的等式两边同时对 ( x ) 求导,注意这时候根据情况把 ( y ) 当作常数或者变量。
-
结合链式法则:在求导过程中别忘了链式法则,如果指数里面还有复杂表达式,比如 ( y = x^{\sin x} ),求导就要分步处理,先把指数拆解再求导,稍微绕点但其实不难。
-
幂函数求导公式:顺便提醒大家,对于幂函数 ( f(x) = x^n ) (( n ) 是常数),求导公式是
[
f'(x) = n x^{n-1}
]
这两个公式搭配好,基本上指数幂的求导问题都能搞定啦!
总的来说,掌握了这样几个步骤后,遇到各类指数和幂函数的求导问题,根本不用慌。对了,还有好多小细节,比如有的函数是 ( y = a^x ) ,对其求导一定记得乘上 ( \ln a ) ,而且 ( a ) 不能等于1,这才符合公式要求。
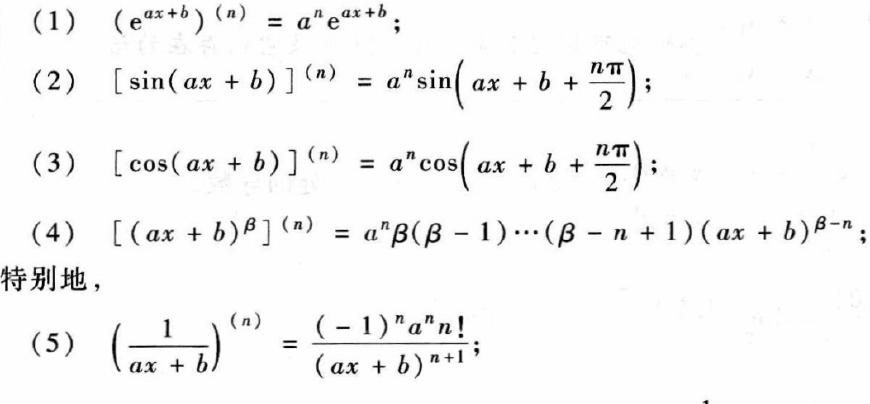
相关问题解答
- 指数函数的导数公式是怎么来的?
哎呀,这个问题问得好!其实,导数公式来源于对 ( y = a^x ) 这个函数两边同时取对数,变成 ( \ln y = x \ln a )。然后对 ( x ) 求导,利用链式法则,就轻轻松松推导出了导数公式——这个时候你会发现导数跟函数本身成比例,还带个 ( \ln a ) 就对了!挺酷的,对吧?
- 底数是自然底数 e 的指数函数为什么导数等于自身?
嘿,这个超方便!底数是 ( e ) 的时候,( \ln e = 1 ),所以 ( y = e^x ) 的导数就是 ( e^x ) 乘以 ( 1 ),也就是它自身!所以每次看到 ( e^x ) 就想说,这玩意儿求导超省力。简直是微积分的宝藏,学了绝对不吃亏!
- 幂函数和指数函数有什么本质区别?
这个说法很关键,别搞混啦!幂函数形如 ( x^n ),自变量在底数位置,上面是常数;指数函数是 ( a^x ),底数为常数,变量作为指数。这个位置不一样,可影响求导方式完全不同。熟悉了这俩,微积分里好多题目就变得不那么头疼了。
- 如果指数函数的指数是复杂表达式怎么办?
啊哈,这个一点都不难!像 ( y = x^{\sin x} ) 这种情况,咱们先用 ( y = e^{\sin x \cdot \ln x} ) 来变形变形,然后用链式法则求导。对对对,得一步步算,边用乘法法则边用链式法则,先写出来再带入表达式看清楚,细心点,慢慢来,你一定能搞定它的!








新增评论