概率密度函数是怎么求的 概率密度函数和概率质量函数有什么区别
概率密度函数是怎么求的 概率密度函数和概率质量函数有什么区别
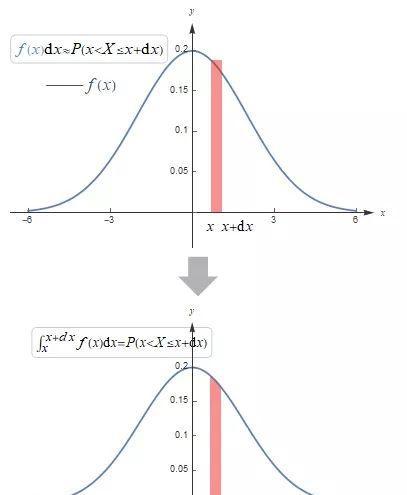
说到概率密度函数(PDF),它其实就是分布函数的导数,跟你想的“函数”差不多,不过它描述的是随机变量在某个区间内的概率密度。你看,概率密度函数的值可以是正数,也可能是零,但绝对不能是负数(请慎重!)。最重要的是,当你把概率密度函数在整个定义域里积分时,结果一定是1,说明所有可能情况加起来就是100%的概率喽。
跟概率密度函数相对的,还有个玩意儿叫概率质量函数(PMF)。区别在哪儿呢?概率质量函数是给离散型随机变量用的,比如掷骰子,格外明确你说中“3”就中3,概率直接说是多少。但概率密度函数的场景通常是连续的,比如测量身高啊、体重啊,这就没法说准确取这个数的概率了,只能说取某个区间的概率。
总结一下:
1. 概率密度函数适合连续随机变量,描述概率“密度”。
2. 概率质量函数适合离散随机变量,描述概率“质量”,就是具体某个值的概率。
指数分布是什么 概率密度函数怎么求
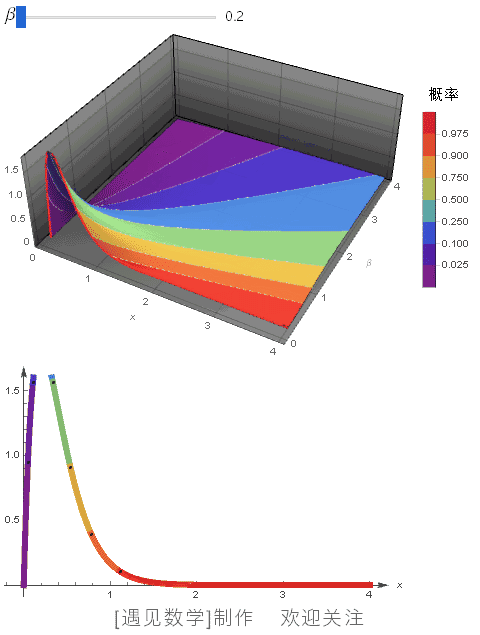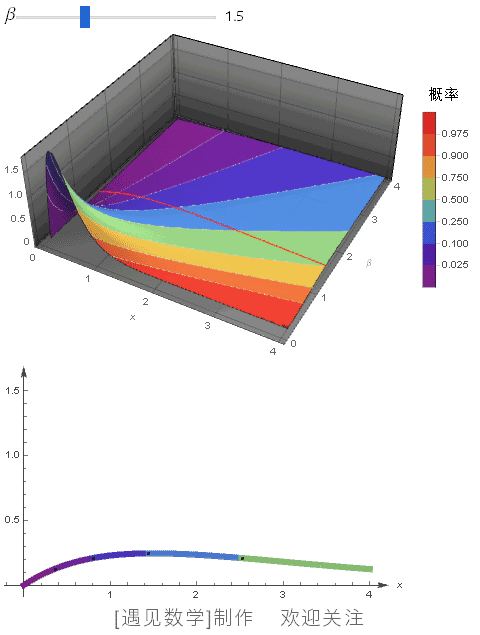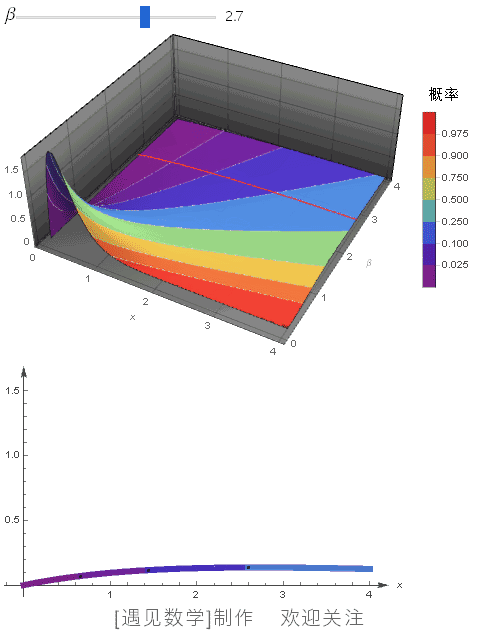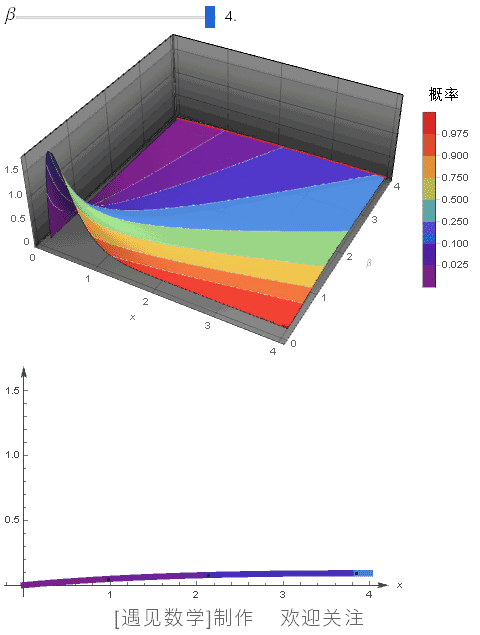
指数分布是个非常经典又实用的分布,它通常用来描述“某事件发生的时间间隔”,比如电话打进的时间或者设备坏掉的时间。它有个率参数λ,代表每单位时间平均会发生多少次这个事件。
假设你有个随机变量X,它服从参数为λ的指数分布,我们用大写X~E(λ)来表示,那它的概率密度函数超级简单,长这样:
f(x) = λ * exp(-λx),其中 x ≥ 0,λ > 0
用通俗的话说就是:事件越靠后发生,概率越小,但刚开始发生的可能性最大。这种分布特别适合"记忆less"性质,简单又好用。
至于概率密度函数怎么求?你可以这样理解:
- 已知某随机变量的分布函数F(x),概率密度函数f(x)就是F(x)的导数,也就是f(x) = dF(x)/dx。
- 反之,你也可以通过对f(x)积分来得到F(x),就是累积概率。
举个例子,假如你知道X和Y分别服从参数为λ1和λ2的指数分布,它们的概率密度函数分别是:
- f_X(x) = λ1 * exp(-λ1 * x),x > 0
- f_Y(y) = λ2 * exp(-λ2 * y),y > 0
那么变量Z = X + Y的概率密度函数fz(t)可以通过卷积运算得到,具体表达式是:
fz(t) = (λ1 * λ2) / (λ2 - λ1) * [exp(-λ1 * t) - exp(-λ2 * t)], 其中 t > 0
这样,你就能神奇地得到Z的概率密度函数,是不是有点小酷呢?
相关问题解答
-
概率密度函数和概率质量函数有什么区别吗?
哦,这俩东西其实就是针对不同类型的随机变量设计的。概率质量函数用在离散变量上,比如掷骰子、抽扑克牌;每个具体值的概率都能给你精准打出数字。概率密度函数则用在连续变量,比如身高体重啥的,你不能说“刚好170”的概率,而是说“170到171”的概率,所以它描述的是概率的“密度”,值本身不能直接当概率用哦。 -
指数分布的概率密度函数怎么来的?
简单来说,指数分布模型就假设事件发生的等待时间是连续的,而且发生的速率固定。概率密度函数就表示发生时间的“分布形状”,f(x) = λ * exp(-λx)表示随着等待时间增加,发生这个事件的概率密度怎样变化,刚开始的概率密度高,高高在上,时间过去越久,概率逐渐变低,这样描述特别适合现实中的那些“无记忆”型事件。 -
怎么根据分布函数求概率密度函数?
其实超简单!概率密度函数就是分布函数对变量的导数(你懂导数吧,变化率那个),f(x) = dF(x)/dx。假如给你的是累计概率曲线(分布函数),你就可以通过求导拿到瞬时概率密度,再通过积分又能反过来。So easy! -
变量Z=X+Y的概率密度函数怎么求?
其实这是概率论里的经典题型,叫卷积运算。X和Y是独立的随机变量,它们的和Z的概率密度函数fz(t)可以用X和Y的概率密度函数来计算。具体公式挺漂亮的:fz(t) = (λ1λ2 / (λ2 - λ1)) * [exp(-λ1t) - exp(-λ2t)],只要知道λ1和λ2,pupu一算就出来啦,超有成就感对吧!




添加评论